If chromatic number is r then the graph is rchromatic. Face colorings of embedded graphs Face colorings of embedded graphs Archdeacon Dan 1984-09-01 000000 We characterize those graphs which have at least one embedding into some surface such that the faces can be properly colored in four or fewer colors.
 Connected Graphs With 5 Vertices And At Least 5 Edges Download Scientific Diagram
Connected Graphs With 5 Vertices And At Least 5 Edges Download Scientific Diagram
A path from a vertex V to a vertex W is a sequence of edges e1e2en such that if Vi and Wi denote the ends of ei then V1 V and Wn W and Wi Vi1 for 1 i nA cycle is a path that involves no edge more than once and V WAny of the vertices along the path can serve as the initial vertex.
Face coloring in graph theory. For a graph G a list assignment Lto the vertices of Gis a kk t-list assignment if every. A face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color. The other graph coloring problems like Edge Coloring No vertex is incident to two edges of same color and Face Coloring Geographical Map Coloring can be transformed into vertex coloring.
A color class of a colored graph is the set of vertices or edges having one particular color. The chromatic number of a graph is the minimum number of colors in a proper coloring of that graph. We say two edges are facially adjacent in a plane graph G if they are consecutive on the boundary walk of a face of G.
Elementary school is a tough time in the lives of many children. 4-color theorem finally proved in 1977 Appel HakenFirst major computer-based proof Optimal 4 coloring. Colorings are a central part of graph theory and over time many variants of proper colorings have been introduced.
The notion of facial edgeface coloring of plane graphs was first introduced by Fabrici Jendrol and Vrbjarová. For example the following can be colored minimum. List coloring and packing coloring.
When a planar graph is drawn without edges crossing the edges and vertices of the graph divide the plane into regions. Embeddings into both orientable and nonorientable surfaces are considered. It has many failed proofs.
A facial parity edge coloring of a 2-edge-connected plane graph is such an edge coloring in which no two face-adjacent edges consecutive edges of a facial walk of some face receive the same. Face Coloring Pages Printable In Graph Theory For Makeup Pictures. The variants we study are packing colorings improper colorings and facial unique-maximum colorings.
Melnikov conjectured that every plane graph is edgeface Δ 3-colourable. For example a loop is a cycle. Most kids report a lot of boredom at school.
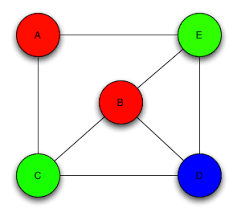
Four color theorem. The smallest number of colors needed to color a graph G is called its chromatic number. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors.
Vertices are assigned the same color. Although recess is fun most of their time is spent doing some things that they find boring. Color to each edge so that no two adjacent edges share the same color and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.
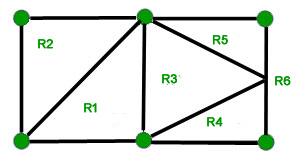
We will call each region a face. In the context of Vizings theorem on edge coloring simple graphs a graph is said to be of class one if its chromatic index equals its maximum degree and class two if its chromatic index equals one plus the degree. Face Coloring.
A packing coloring of a graph Gis an assignment of colors 1kto the vertices of. In graph theory graph coloring is a special case of graph labeling. The Four Color Theorem 23 integer n.
Kids Face Coloring Page. The number of faces does not change no matter how you draw the graph as long as you do so without the edges crossing so it makes sense to ascribe the number of faces as a property of the planar graph. It is an assignment of labels traditionally called colors.
They hate homework and would rather be playing outside. We consider two branches of coloring problems for graphs. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraints.
A triangle a square. Saturday February 22nd 2020. We introduce a new variation to list coloring which we call choosability with union separation.
In graph theory graph coloring is a special case of graph labeling. According to Vizings theorem all simple graphs are either of class one or class two. Face coloring in graph theory worksheet pictures girl kids page smiley happy for glasses house.
Graph Theory - Coloring. In its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color. Francis Guthrie 1852 The four color map theorem states that given any separation of a plane into contiguous regions producing a figure called a map no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color.
The graph above has 3 faces yes we do include the outside region as a face. The edgeface colouring of plane graphs was first studied in and for 3- and 4-regular graphs. Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints.
This is called a vertex coloring. The conjecture was confirmed independently by Sanders and Zhao and Waller.
 Selection 004 Planar Graph Graphing Graph Creator
Selection 004 Planar Graph Graphing Graph Creator
 Application Of Planar Graph In Real Life Blog Lif Co Id
Application Of Planar Graph In Real Life Blog Lif Co Id
 Spring Of Mathematics Graphing Geometry Pattern Amazing Mathematics
Spring Of Mathematics Graphing Geometry Pattern Amazing Mathematics
 Graph Of 9 Vertices And 12 Edges Drawn In Geogebra Download Scientific Diagram
Graph Of 9 Vertices And 12 Edges Drawn In Geogebra Download Scientific Diagram
 Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
 Application Of Planar Graph In Real Life Blog Lif Co Id
Application Of Planar Graph In Real Life Blog Lif Co Id
The 16 Connected 4 Regular Graphs On 9 Vertices Download Scientific Diagram
 Graph Theory Graphing Geometric Geometric Tattoo
Graph Theory Graphing Geometric Geometric Tattoo
 Mathematics Graph Theory Basics Set 2 Geeksforgeeks
Mathematics Graph Theory Basics Set 2 Geeksforgeeks
 Overview Of Graph Colouring Algorithms
Overview Of Graph Colouring Algorithms
 Pdf An Introduction To Graph Theoretical Methods In Geography
Pdf An Introduction To Graph Theoretical Methods In Geography
 Graph Coloring Wikipedia Np Complete Problems In Graph Theory Cse 421 Algorithms Richard Anderson Lecture 29 Complexity Theory Np Completeness Algorithms
Graph Coloring Wikipedia Np Complete Problems In Graph Theory Cse 421 Algorithms Richard Anderson Lecture 29 Complexity Theory Np Completeness Algorithms
 Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
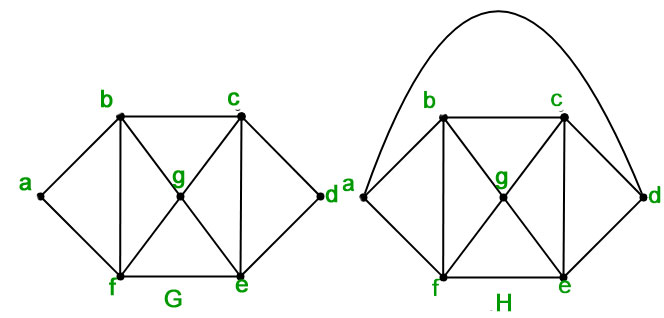
 Graph Coloring And Chromatic Numbers Brilliant Math Science Wiki
Graph Coloring And Chromatic Numbers Brilliant Math Science Wiki
 Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
Mathematics Planar Graphs And Graph Coloring Geeksforgeeks
 Wheel Graph From Wolfram Mathworld
Wheel Graph From Wolfram Mathworld
 3 Node Subgraphs Triangle Tattoo Crystals Graphing
3 Node Subgraphs Triangle Tattoo Crystals Graphing
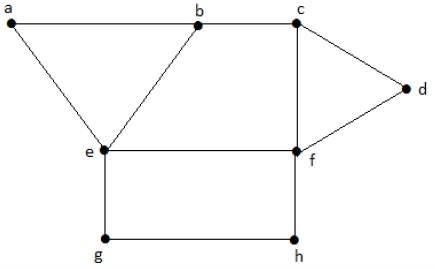 Graph Theory Coloring Tutorialspoint
Graph Theory Coloring Tutorialspoint
 Finding Face Vertices From The Face Adjacency Graph Mathematica Stack Exchange Graphing Vertex Planar Graph
Finding Face Vertices From The Face Adjacency Graph Mathematica Stack Exchange Graphing Vertex Planar Graph
 Example Graph Maximum Clique The Number Of Vertices Of A Maximum Download Scientific Diagram
Example Graph Maximum Clique The Number Of Vertices Of A Maximum Download Scientific Diagram
 Overview Of Graph Colouring Algorithms
Overview Of Graph Colouring Algorithms

0 Comments